一、0.1 + 0.2 != 0.3 的解释

我们小学就知道 0.1+0.2=0.3，但是作为大学毕业或者还没毕业的你你知道 0.1+0.2!=0.3吗？

首先我们要知道计算机中只能进行二进制的运算，我们在输入 0.1 时会转换为二进制，0.2也是一样的会转换为二进制，然后才进行相加运算。

浮点数转换为二进制的规则：整数部分和小数部分分离开，整数部分的转换规则是：除以2取余，然后逆序排序。小数部分转为二进制规则是：乘以2取整数部分，然后用小数部分再乘以2取整数部分，一直直到结果为0，正序排序。

例如：0.1 在计算机中的存储。

0.1 * 2 = 0
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1

由于计算机的内存是有限的，不能无限存储下去，所以我们需要攫取一部分，比如我们使用的是 Java 中的 double 类型存储，那么是8个字节，也就是64bit，所以保留64位数。

这里由于 0.1 在计算机中无法完全转换为二进制，同理 0.2 也是无法转换为精确的二进制数的，所以在进行相加运算之前就已经不精确了，在相加之后也可能不精确。

我们来看一下在 Java 中运行的结果。

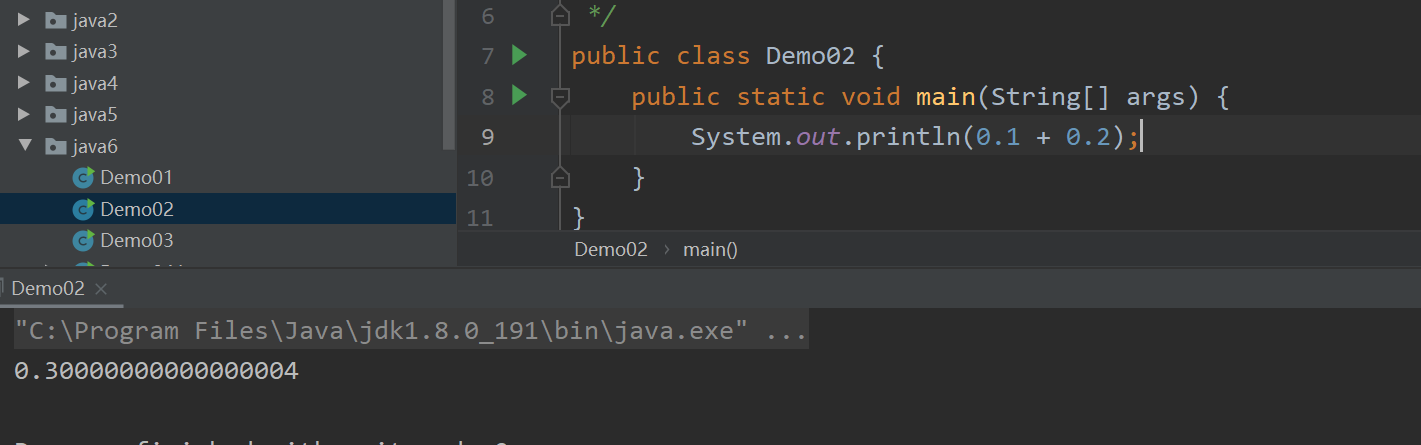
image-20230405131215548

其实这与使用的编程语言无法，而是与计算机底层存储数据有关，因为计算机只能看懂二进制数据，而看不懂十进制数据。无论你使用什么编程语言都要转换为二进制然后再运算。

比如这里我使用 Python 语言来测试一下，结果发现 0.1+0.2 也是不等于 0.3的。

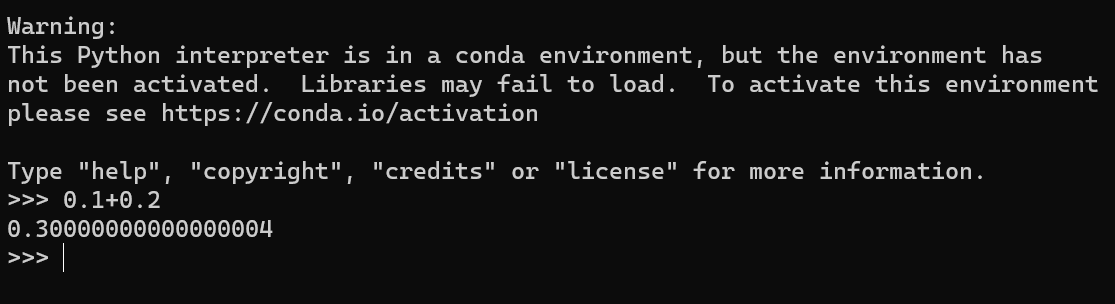
image-20230405131630182

二、解决方案

我们在某些情况下，我们的计算结果要求是准确的，比如在航天系统中，计算的结果不能有一丝的误差。这里我讲解的使用在 Java 中的解决方案，其它编程语言的解决方案，你们可以自行网上搜索。

在 Java 中可以使用 BigDecimal 类中的方法来计算。

public static void main(String[] args) {
    BigDecimal a = new BigDecimal("0.1");
    BigDecimal b = new BigDecimal("0.2");
    System.out.println(a.add(b));
}

通过以上的代码运行的结果就是准确的结果 0.3。

这是面试或笔试中会被问到的题目，这里做一下简单的总结，如果本篇文章对你有用，记得收藏。更多内容可以访问我的博客。

Q.E.D.

热爱生活，热爱程序