树

定义：Tree是n(n>=0)个结点的有限集

若n=0，称为空树

若n>0，则它满足如下两个条件：

• 有且仅有一个特定的称为根(Root)的结点
• 其余结点可以分为m(m>=0)个相互不相交的有限集T1,T2,T3…Tm，其中每一个集合本身又是一棵树，并称为根的子树(SubTree)

树定义是一个嵌套的定义

树的表示形式：

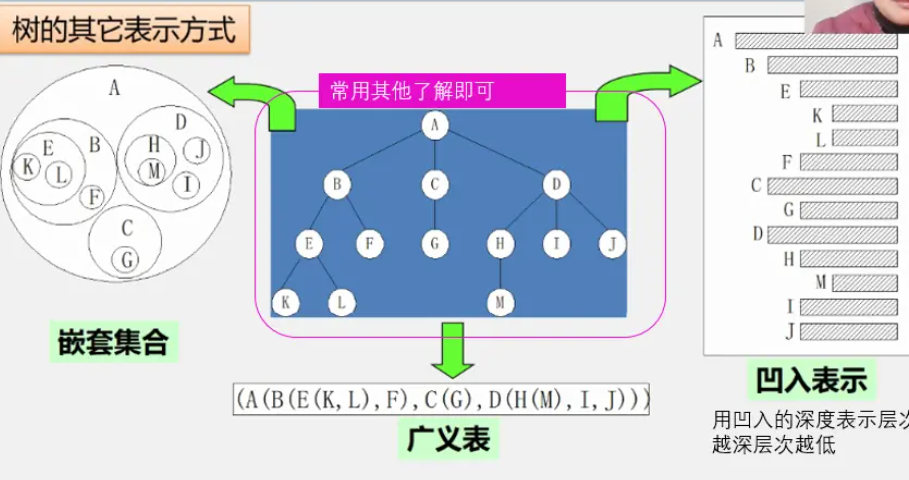
树的相关概念:

结点的度：结点拥有的子树数

树的度：树内各结点的度的最大值

树的深度：树中结点的最大层次（有多少层）

树结构和线性结构的对比

二叉树

注意：二叉树不是树的一种特殊情况。

二叉树定义：由空集或由一个根结点以及两棵互不相交的左右子树组成。

特点：

1. 每个结点最多有两个孩子
2. 子树有左右之分，次序不能颠倒
3. 二叉树可以是空集合，根可以有空的左子树或空的右子树。

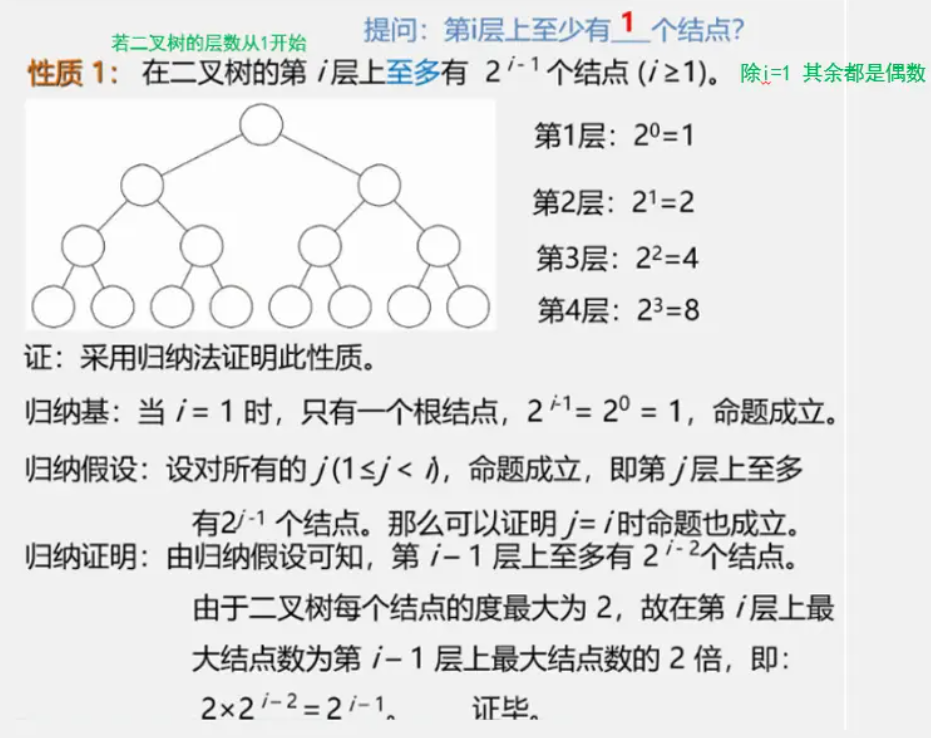
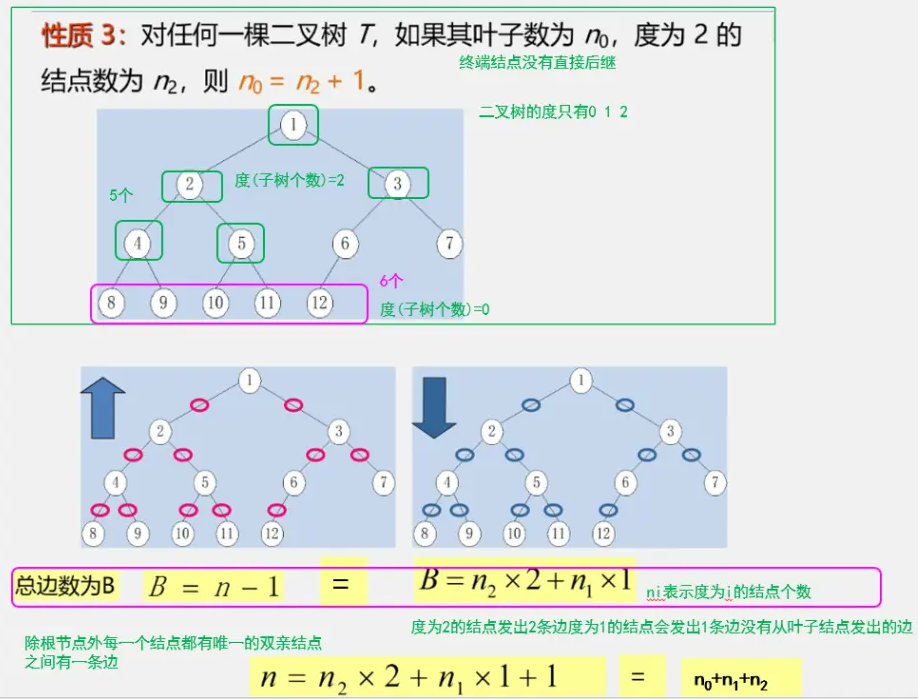
二叉树的性质

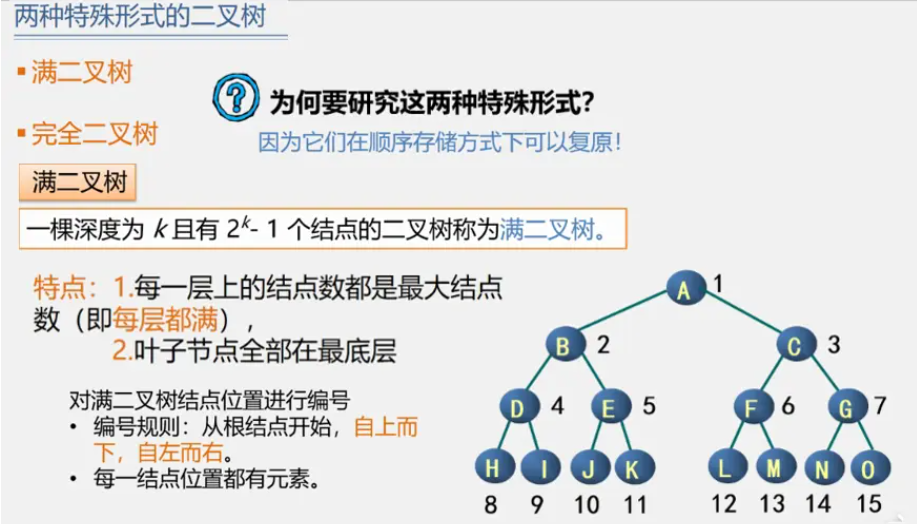
两种特殊的二叉树

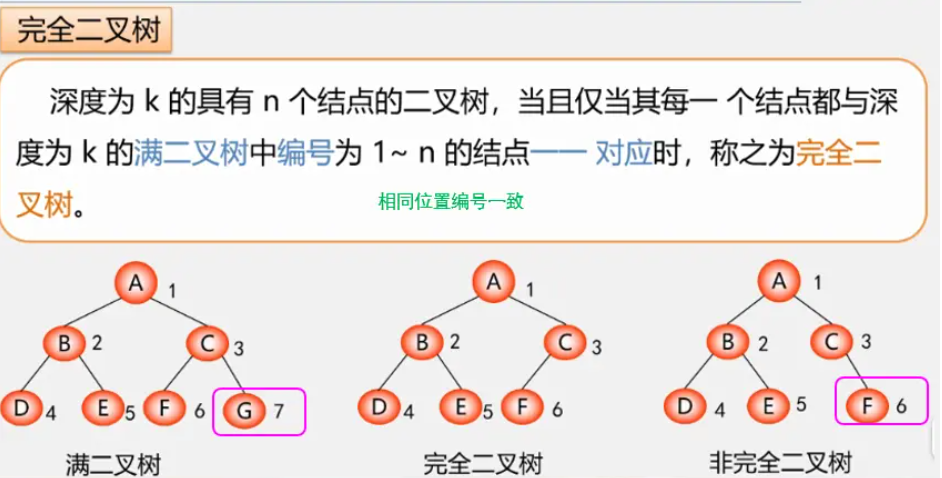
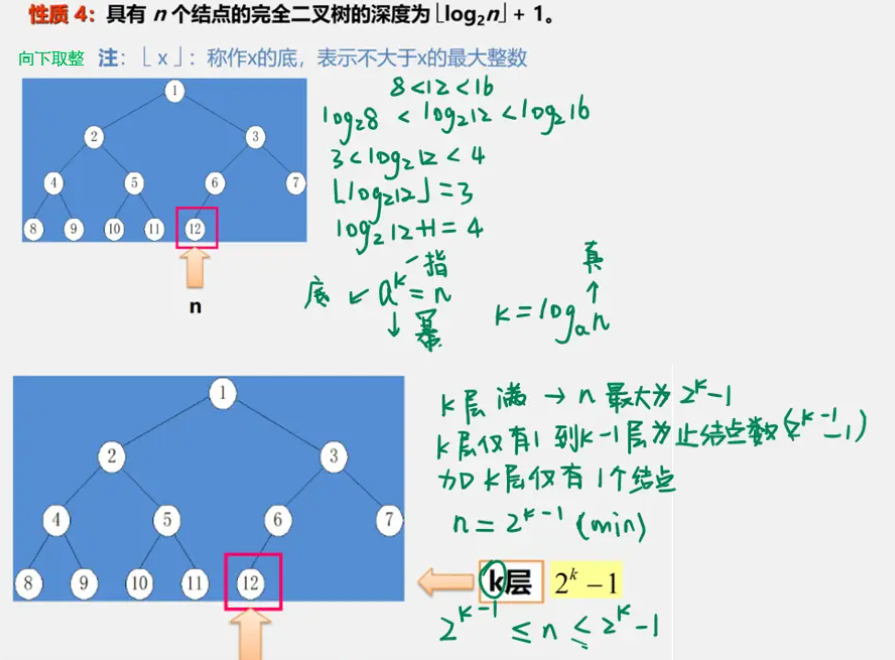
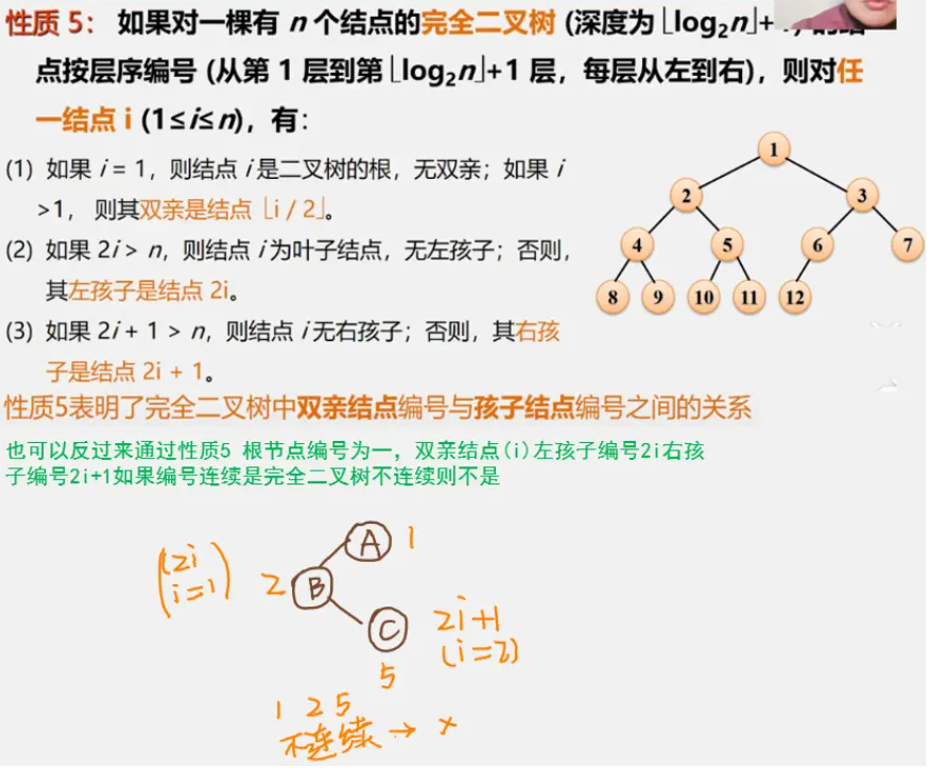
二叉树的存储结构

顺序存储

按照满二叉树的结点层次编号，依次存放二叉树中的数据元素。

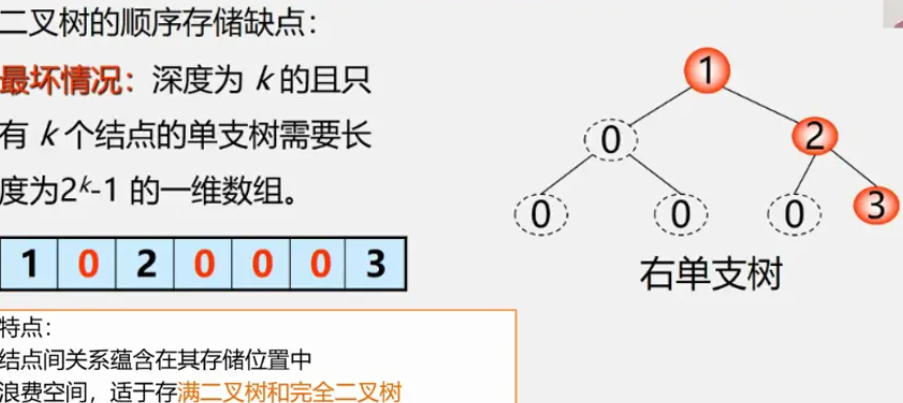
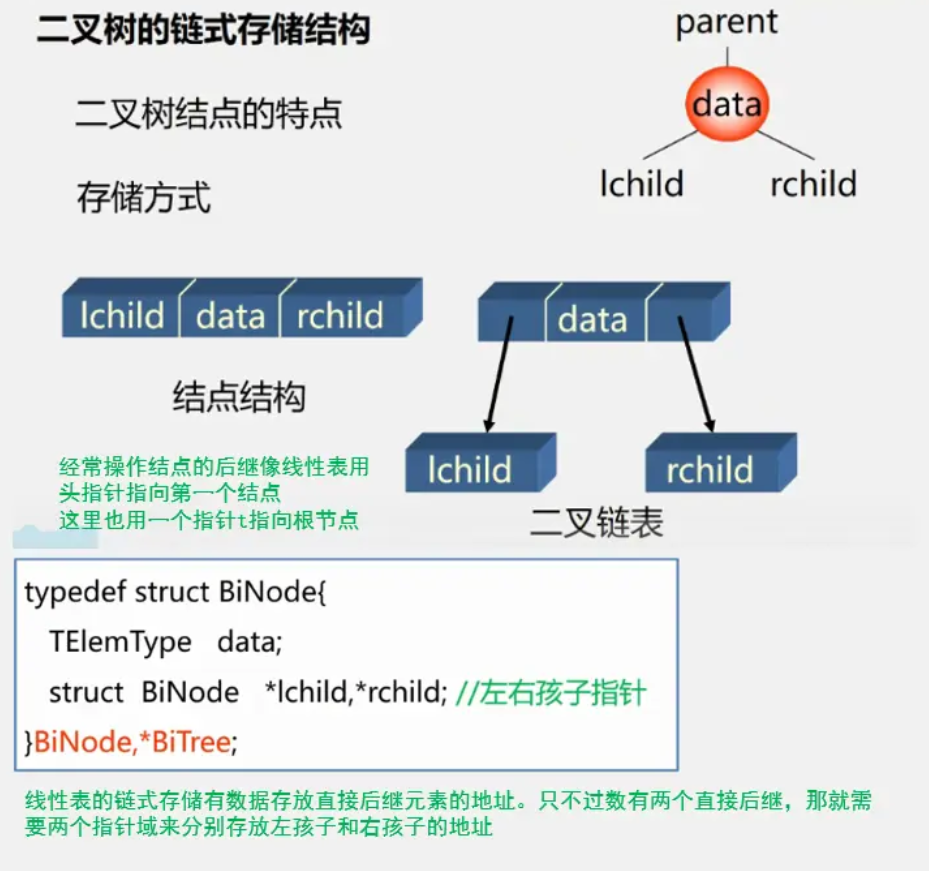
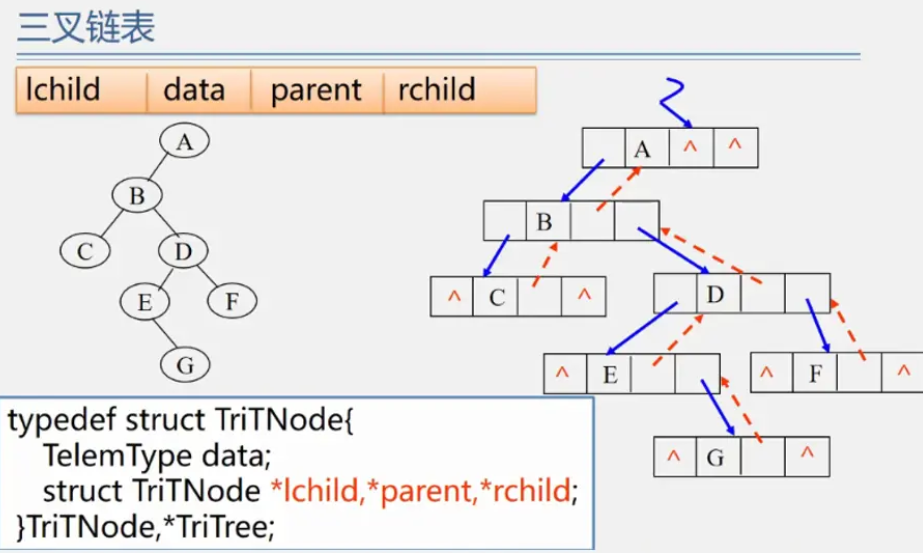
二叉树的链式存储结构

二叉树的遍历

定义：是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次

二叉树的遍历方式（左-右）

二叉树的遍历方式有很多，如果我们限制了从左到右的习惯方式，那么主要就分为四种。

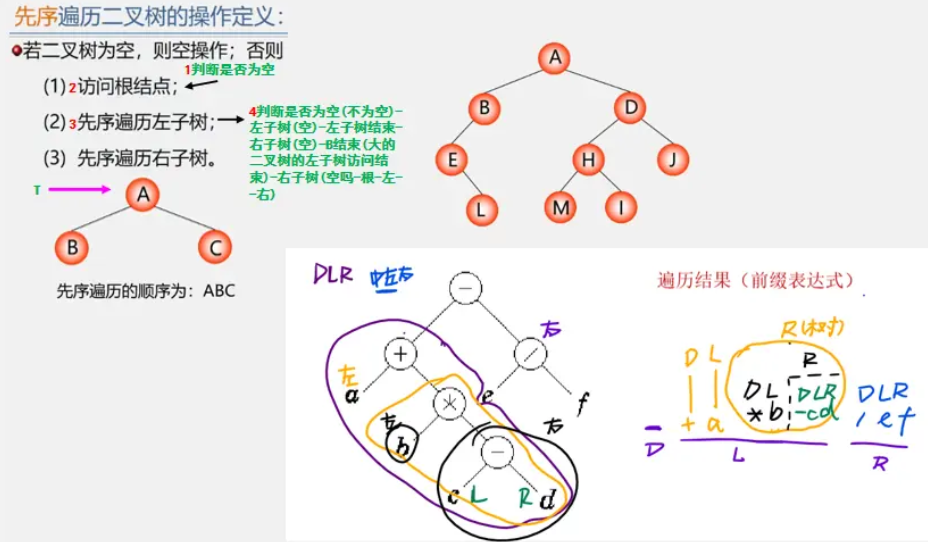
1. 先序遍历

先要判断是否为空树，如果是，则直接返回空操作。

否则进行如下操作：

先访问根结点

然后遍历左子树

最后遍历右子树

（根-左-右）

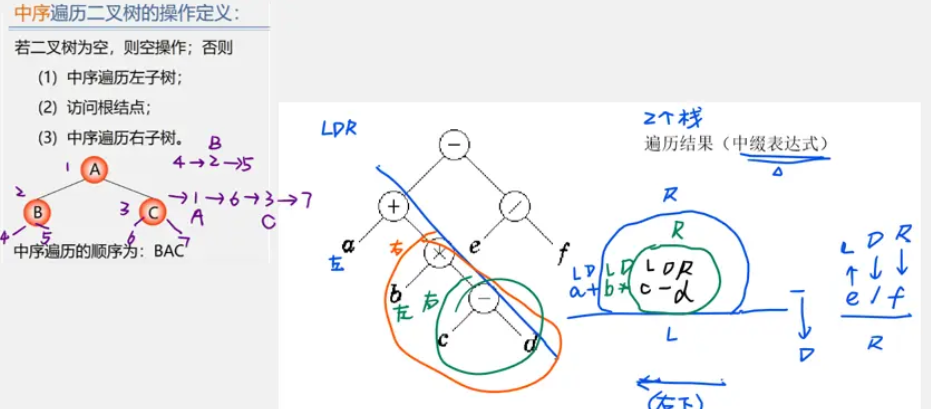
2. 中序遍历

先要判断是否为空树，如果是，则直接返回空操作。

否则进行如下操作：

从根结点开始（注意并不是先访问根节点）

先遍历根结点的左子树

然后再访问根结点

最后遍历右子树

（左-根-右）

3. 后序遍历

先要判断是否为空树，如果是，则直接返回空操作。

否则进行如下操作：

先左，后右，最后根

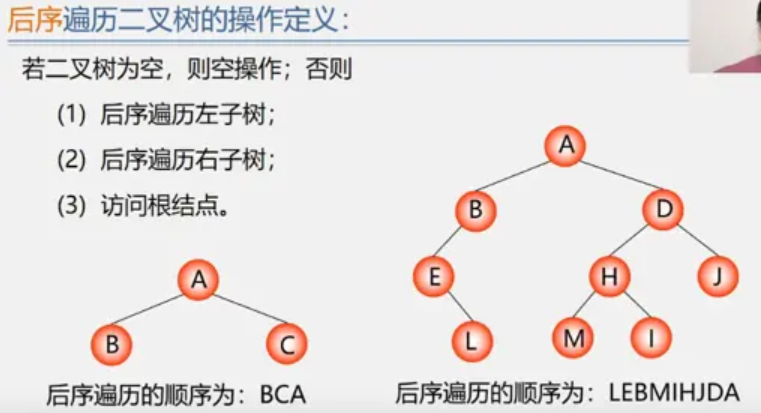
4. 层次遍历

先要判断是否为空树，如果是，则直接返回空操作。

否则进行如下操作：

从树的第一层，即根结点开始访问

按照从上到下逐层遍历

同一层中则按照从左到右逐个访问结点

构造二叉树

知道先序序列和中序序列可以构造二叉树，如图所示。

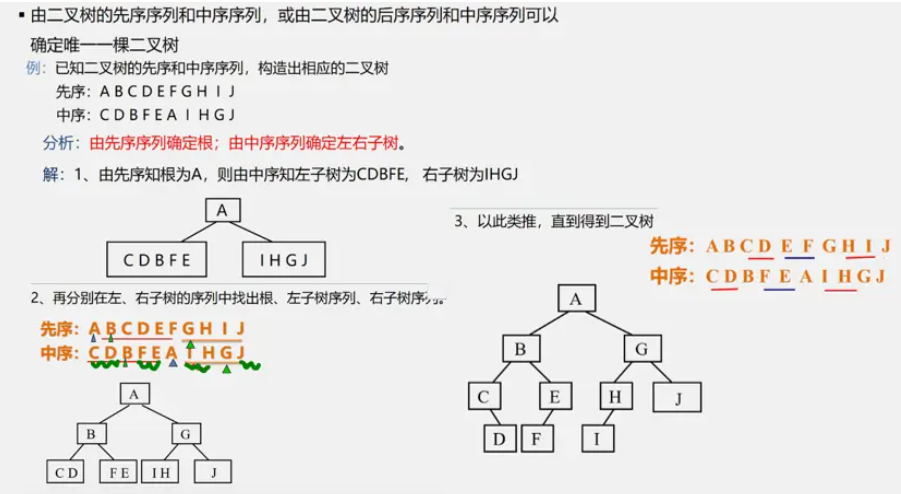
知道后序序列和中序序列，可以构造二叉树，如图所示。

二叉树的算法实现

构造一棵二叉树

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

先序遍历

递归算法实现

public class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        preorder(root, res);
        return res;
    }

    //递归算法
    public void preorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }
}

迭代算法实现

public class Solution2 {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>(); //存放结果
        Stack<TreeNode> stack = new Stack<>(); //存放节点

        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                res.add(root.val);
                stack.add(root);
                root = root.left;
            }
            root = stack.pop().right;
        }

        return res;
    }
}

中序遍历

递归算法实现

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inorder(root, list);
        return list;
    }

    public void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}

迭代算法实现

public class Solution2 {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        //创建一个栈
        Stack<TreeNode> stack = new Stack<>();
        //当前指向的节点root和栈都为空时，才结束遍历
        while (root != null || !stack.isEmpty()) {
            //当当前节点为空时，出栈，否则入栈
            while (root != null) { //把左边子树都遍历完成，把左子树中的每个根节点入栈保护起来
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            //出栈的节点的值就是当前要访问的值
            list.add(root.val);
            root = root.right;
        }
        return list;
    }
}

后序遍历

递归算法实现

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }

    //递归法
    public void postorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        postorder(root.left, res);
        postorder(root.right, res);
        res.add(root.val);
    }
}

迭代算法实现

class Solution2 {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>(); //存放结果集
        Stack<TreeNode> stack = new Stack<>(); //暂存节点
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                //先按照根右左顺序遍历，然后进行反转，就变成左右根顺序了
                res.add(root.val); //把当前指向的节点的值放到集合中
                stack.push(root); //把右子节点都入栈，先入栈的后弹出
                root = root.right; //改变指向
            }
            //经过上面的while循环，root已经指向树的最右边的叶子节点
            TreeNode cur = stack.pop(); //出栈叶子节点的双亲节点
            root = cur.left; //双亲节点的左子节点
        }
        //因为是根据 根-右-左 顺序来遍历的，所以需要反转结果集
        Collections.reverse(res);
        return res;
    }
}

层次遍历

public class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root); //添加根节点
        while (!queue.isEmpty()) {
            List<Integer> list = new ArrayList<>();
            int curLevelNum  = queue.size(); //当前层的节点个数
            for (int i = 0; i < curLevelNum ; i++) { //遍历当前层
                TreeNode curNode = queue.removeFirst(); //移除队首节点
                list.add(curNode.val); //把队首节点的值添加到临时集合list中
                if (curNode.left != null) { //移除队首节点时，同时把左右节点都入队
                    queue.add(curNode.left);
                }
                if (curNode.right != null) {
                    queue.add(curNode.right);
                }
            }
            res.add(list);
        }
        return res;
    }
}

输出的结果

如果要输出[1, 2, 3, 4, 5]的形式，需要把for循环去掉

扩展

N叉树的层次遍历

public class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
}

public class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return new ArrayList<>();
        }
        Queue<Node> queue = new LinkedList<>(); //定义一个双端队列
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> temp = new ArrayList<>(); //保存每层中节点的值
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node node = queue.poll();
                temp.add(node.val);
                for (int j = 0; j < node.children.size(); j++) {
                    if (node.children.get(j) != null) {
                        queue.offer(node.children.get(j));
                    }
                }
            }
            res.add(temp);
        }
        return res;
    }
}

二叉树的锯齿形层序遍历

public class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return new ArrayList<>();
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int index = 1; //层次
        while (!queue.isEmpty()) {
            List<Integer> temp = new ArrayList<>();
            int size = queue.size();
            for (int i = 0; i < size; i++) { //遍历当前层中的节点
                //为什么不用remove方法，因为当队列为空时，remove方法会报异常，poll方法会返回null
                TreeNode node = queue.poll();
                temp.add(node.val); //把当前节点值保存起来
                //如果左节点不为空，则放到队列中，充当下次遍历的节点
                if (node.left != null) {
                    //为什么不用add方法，因为当队列满时，add方法会报异常，offer方法会返回false
                    queue.offer(node.left);
                }
                //如果右节点不为空，则放到队列中，充当下次遍历的节点
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            //判读是单数层还是双数层，单数层遍历方向为从左到右顺序
            if ((index & 1) == 1) {
                res.add(temp);
            } else {
                Collections.reverse(temp); //双数层时，需要反转
                res.add(temp);
            }
            index++;
        }
        return res;
    }
}

Huffman树

定义

给定n个权值作为n个叶子结点

构造一棵二叉树，如果树的带权路径长度达到最小，则这棵树被称作哈夫曼树。

权(weight): 将树中结点赋给一个有着某种含义的数值，(具体的意义根据树使用的场合确定)则这个数值称为该结点的权。

结点的带权路径长度：从根结点到该结点之间的路径长度与结点上权的乘积。

树的带权路径长度：从树根到每一个结点的路径长度之和

构造哈夫曼树的算法

1. 构造森林全是根

   

2. 选用两小造新树

   

3. 删除两小添新人

   

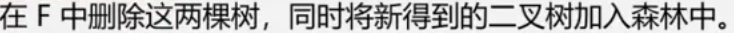
4. 重复2，3剩单根

总结

包含n棵树的森林要经过n-1次合并才能形成哈夫曼树，共产生n-1个新结点

所以哈夫曼树的总的结点数是n+n-1=2n-1个结点。

哈夫曼树的结点度为0或度为2，没有度为1的结点。

权值越大离根越近，权值越小离根越远。

Huffman编码

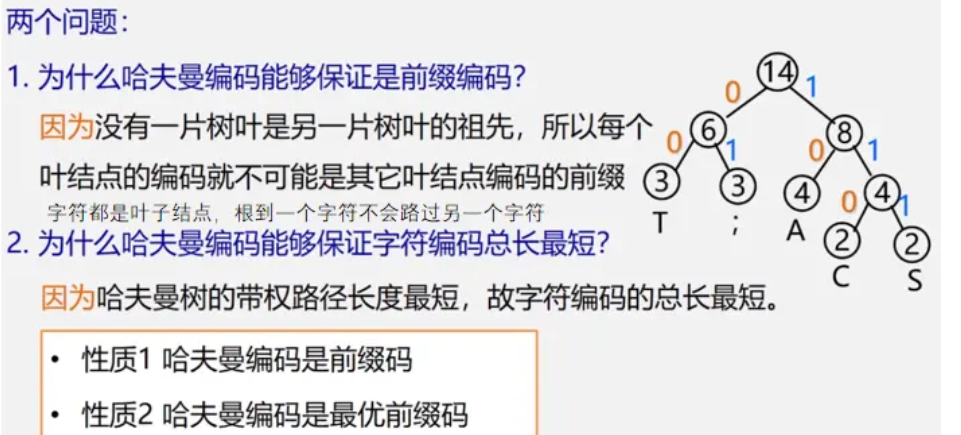
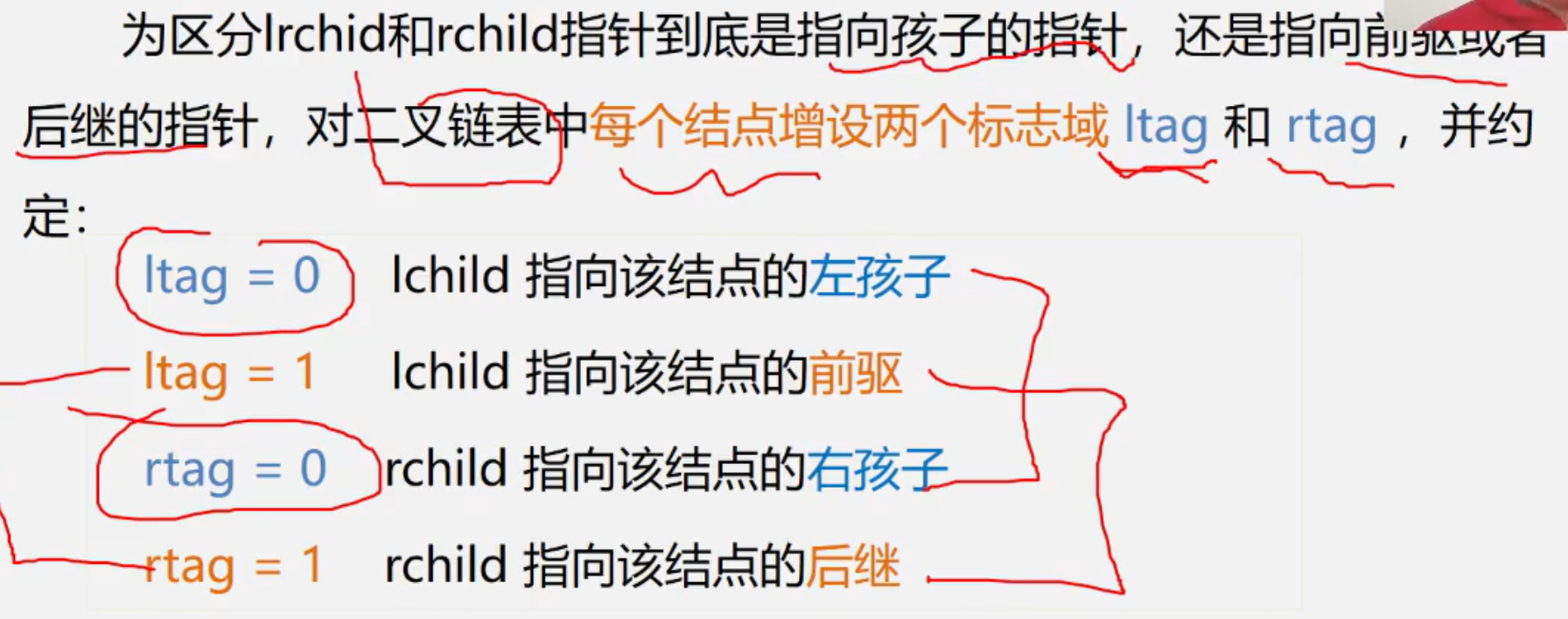
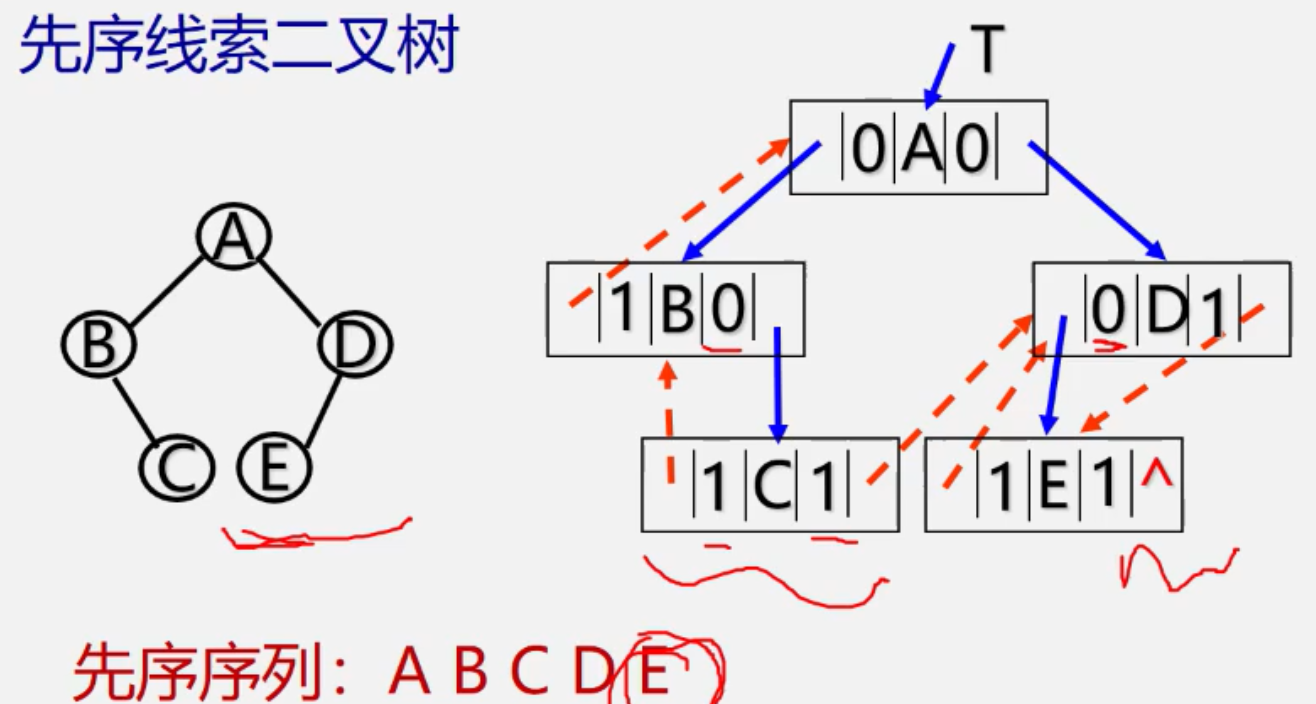
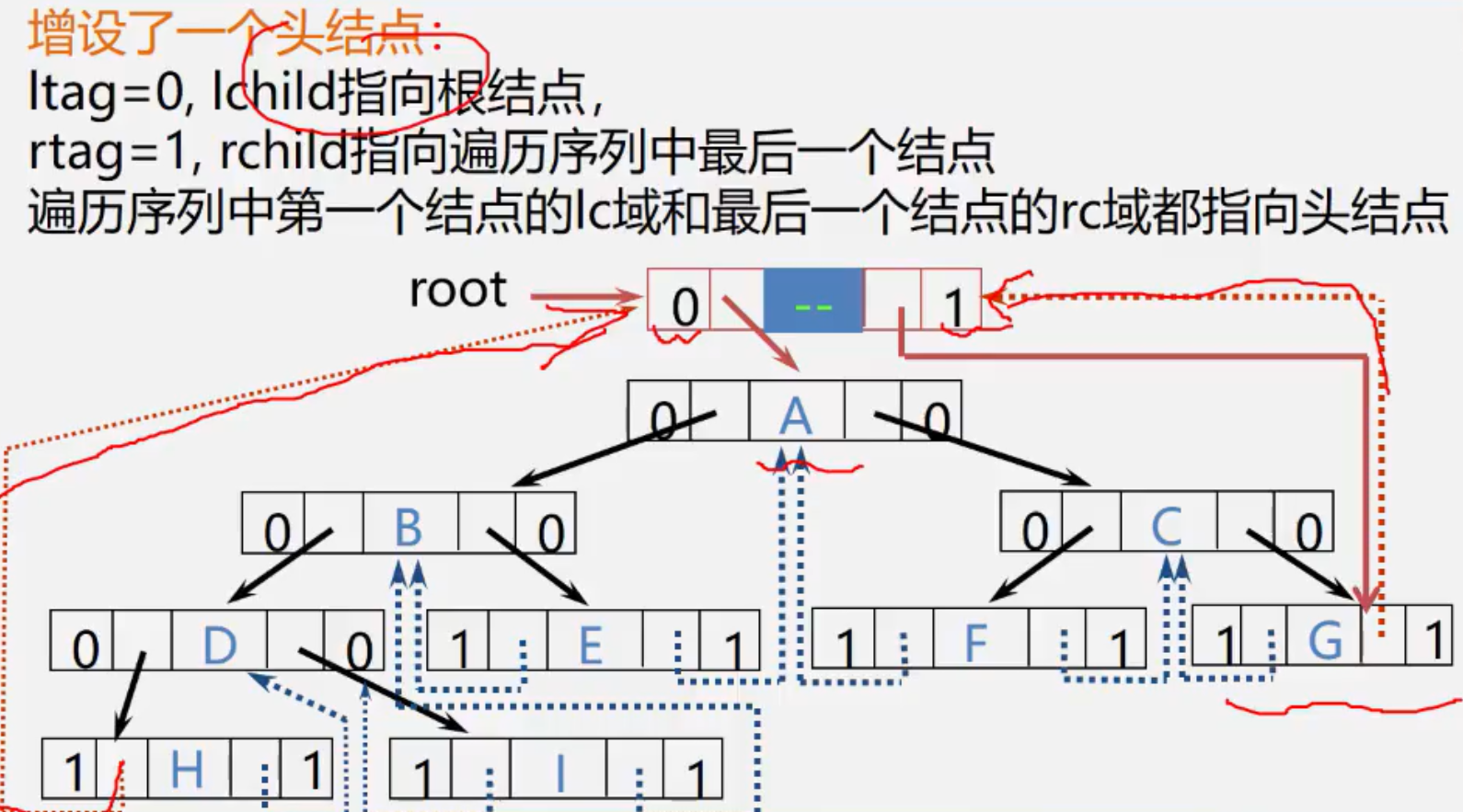
线索二叉树

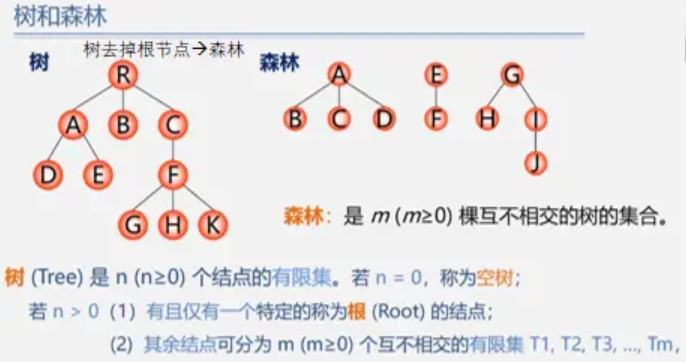
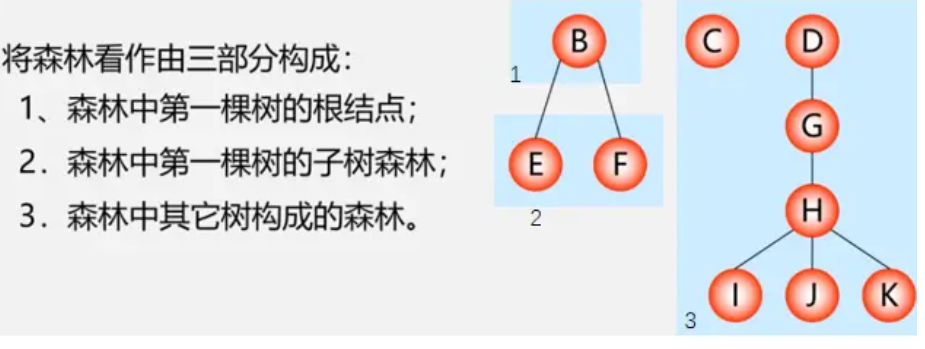
树与森林

树一定是森林，但森林不一定是树

树的表示方法

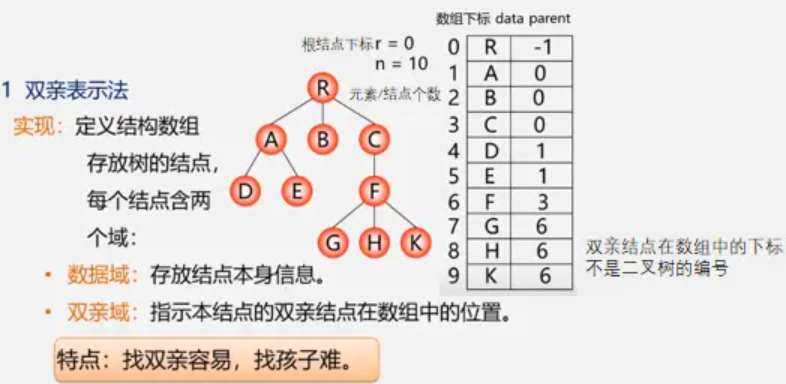
双亲表示法

定义结构数组存放树的结点，每个结点含两个域。

数据域：存放结点本身信息。

双亲域：指示本结点的双亲结点在数组中的位置。

特点：找双亲容易，找孩子难。

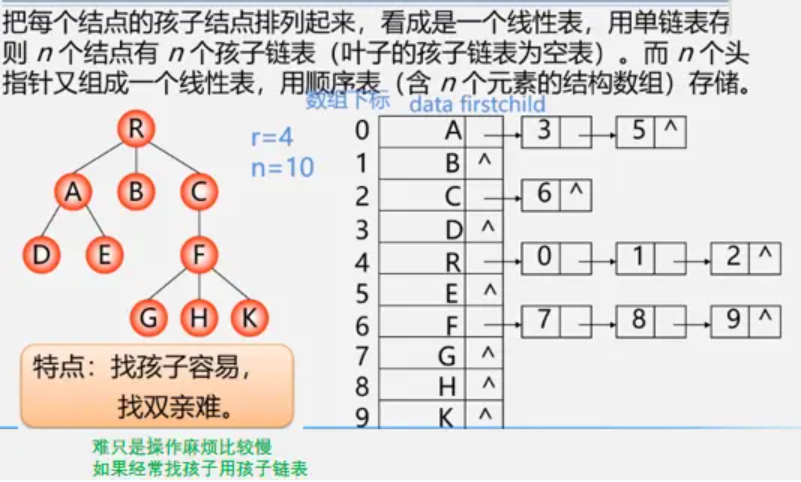
孩子链表

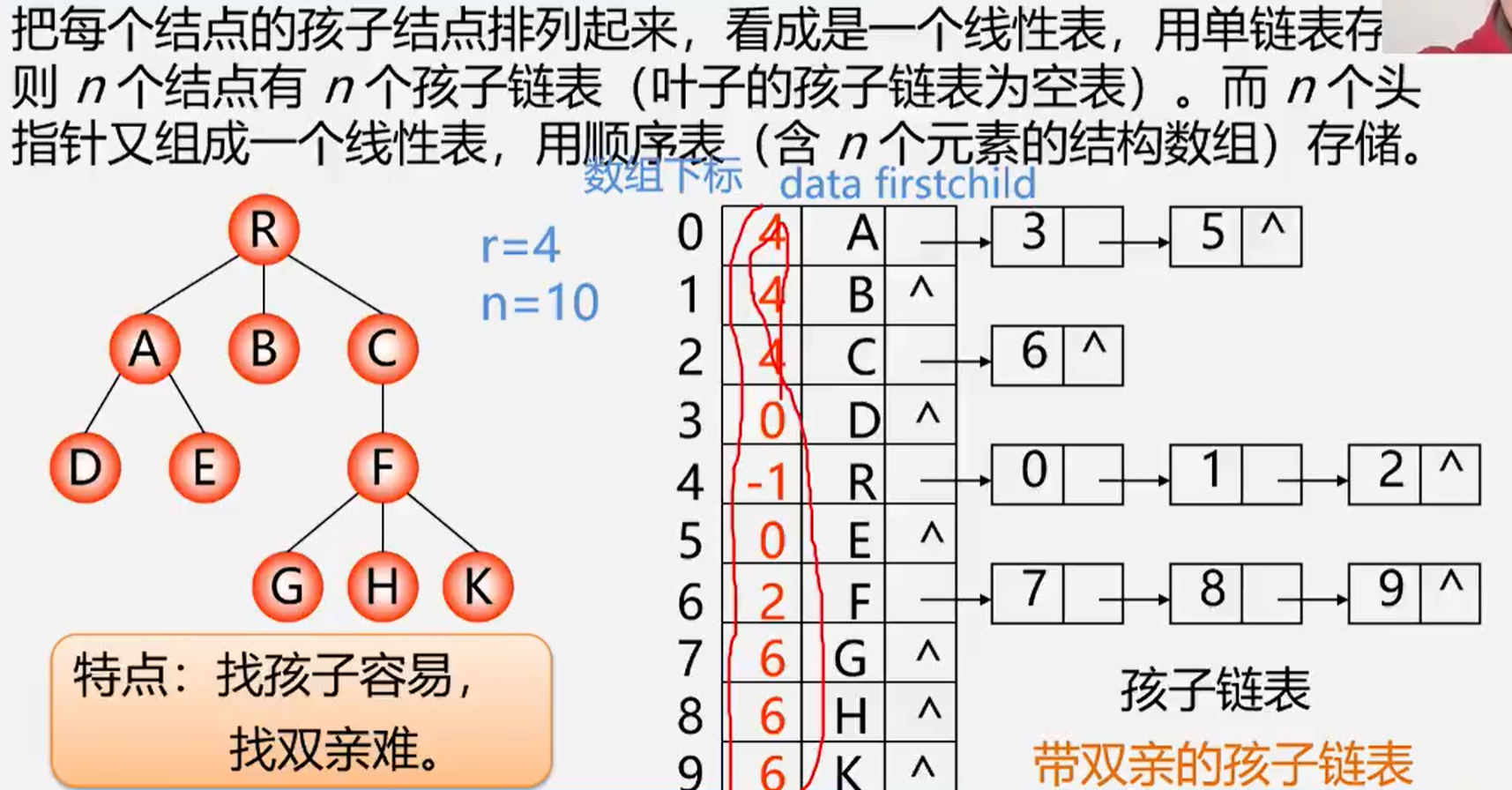
带双亲的孩子链表

孩子兄弟表示法

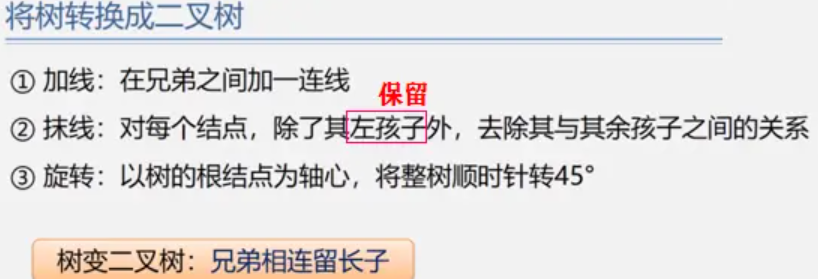
树与二叉树的转换

树转二叉树

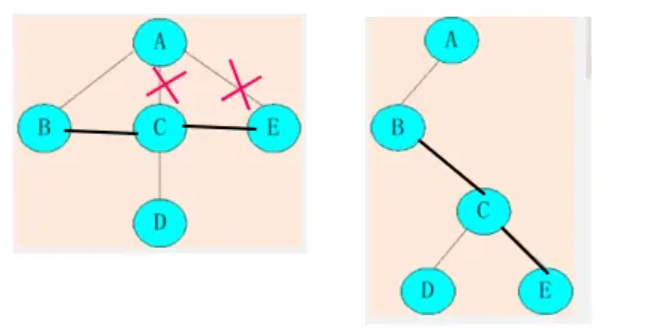
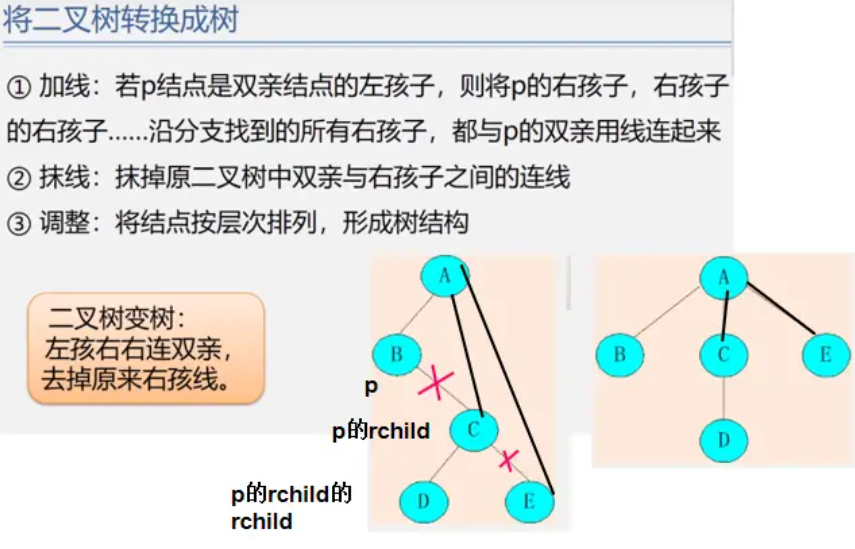
二叉树转树

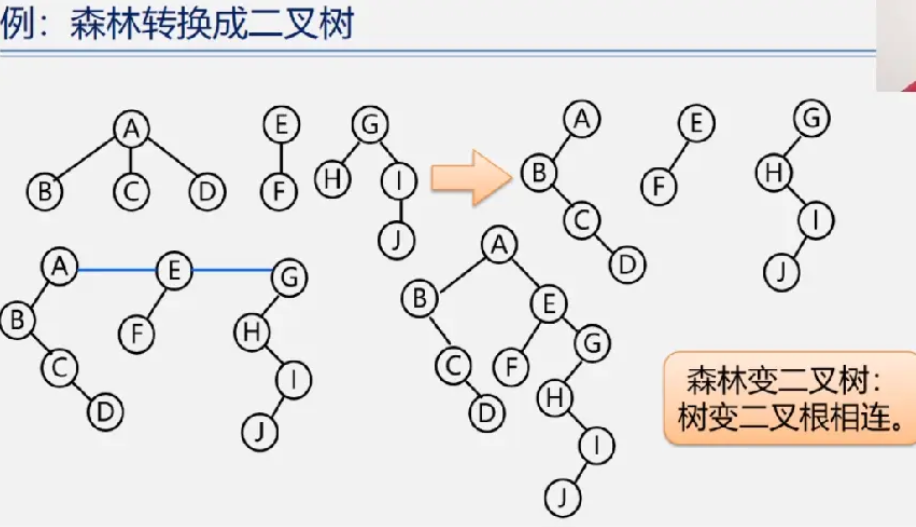
森林与二叉树的转换

森林转二叉树

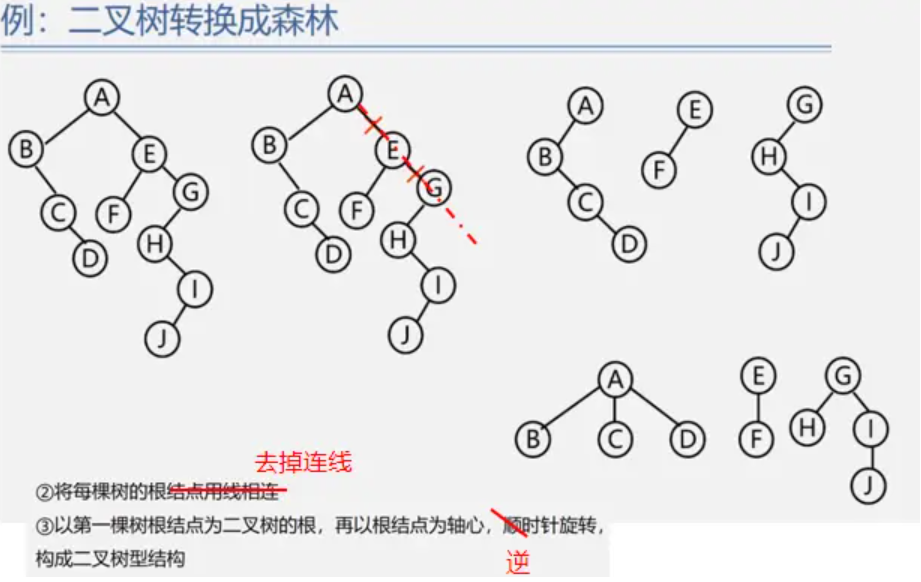
二叉树转森林

树与森林的遍历

树的遍历

有三种遍历方式：

1. 先根遍历：若树非空，则先访问根结点，然后依次先遍历各棵子树。
2. 后根遍历：若树非空，则先依次后根遍历各棵子树，然后访问根结点。
3. 层次遍历：若树非空，则自上向下自左向右访问树中的每个结点。

森林的遍历

Q.E.D.